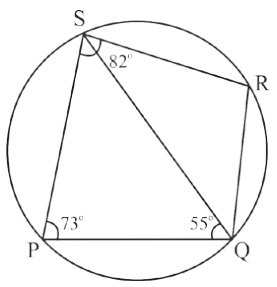
PQRS is a cyclic quadrilateral. Given $ \angle QPS = 73^{\circ}, \angle PQS = 55^{\circ} $

Geometry (10)

PQRS is a cyclic quadrilateral. Given $ \angle QPS = 73^{\circ}, \angle PQS = 55^{\circ} $ and $\angle PSR = 82^{\circ} $, calculate:

i.   $\angle QRS $
ii.  $\angle RQS $
iii. $\angle PRQ $

Answer

(opposite angles of a cyclic quadrilateral are supplementary)

i.  $\angle QRS = 180^{\circ} –  73^{\circ} = 107$

ii. $\angle RQS = 180 –  (82^{\circ} + 55^{\circ})$
     = 180 – 137
     = $43^{\circ}$

iii. $\angle PSQ = 180^{\circ} – (73^{\circ} + 55^{\circ})$
     = $52^{\circ}$

∴  $\angle PRQ = \angle PSQ = 52^{\circ}$

(∠s in the same segment are equal)