In ∆PQR, MN is parrallel to QR and

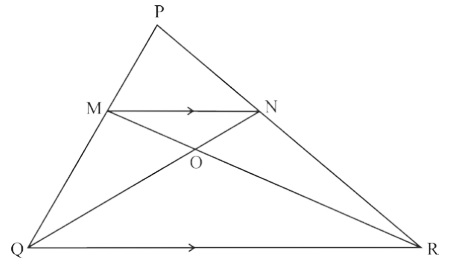
In ∆PQR, MN is parrallel to QR and $\frac {𝑃𝑀}{𝑀q}=\frac{2}{3}$

i. $Find \frac{𝑀N}{𝑄R}$
ii. Prove that ∆OMN and ∆ORQ are similar.
iii. Find, Area of ∆OMN : Area of ∆ORQ

Answer

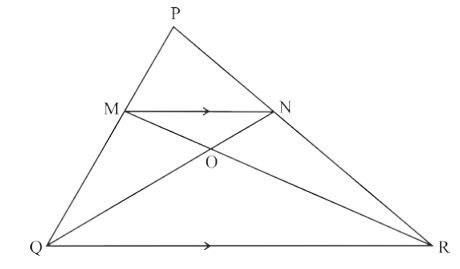
Proving ∆PMN ~ ∆PQR
i.  $\frac{MN}{QR}=\frac{2}{5}$
ii. ∠MON = ∠QOR (vertically opposite angles)
∠MNO = ∠OQR (alternate angles)
∠NMO = ∠ORQ (3rd angle)
iii. ar ∆OMN: ar ∆ORQ = 4 : 25